With the popularity of the Dividend Toolkit, I often get questions by email regarding what is a “fair” discount rate to use to calculate the present value of a stock.
First, I must warn you that stock valuation is sitting on the line separating science and magic: there is a big part of work that involves the rationale & justification of the usage of a specific discount rate, but there is also the magic of events happening on the stock market putting our decision to the test. I guess the most important part is to understand the effect of the discount rate in our calculation and to clearly establish what discount rate to use to calculate the fair value of a stock. If our methodology is consistent from one calculation to another, our overall investment process will make sense and we won’t be making too many mistakes.
The Idea behind Discounting
This brings up the purpose of discounting. The discount rate is used to calculate how much the money you will receive tomorrow is worth today. In other words: how much should you pay today for an asset that will pay you back later.
You have to discount the future money by an appropriate value in order to translate it into today’s value. How much you discount it by can vary. You could, for example, use a “risk-free” rate of return, such as the yield on a U.S. Government Treasury Bill. Or, you could use Weighted Average Cost of Capital (WACC). More appropriately (and simply) in my view, what you should usually use is your targeted rate of return, which would naturally be at a premium to whatever the current risk free rate of return is. This spares you from making a series of calculations and gets straight to the point.
If you want to get, say, a 10% rate of return on your money, then you should use a discount rate of 10% per year when translating future dollars into present dollars. You may also alter it depending on your estimation of the level of risk involved. For a higher risk investment I’d use a higher discount rate (perhaps 12% or so), while in the case of a very defensive and reliable business I may use a discount rate of 8%. It could also be tied to the current risk free rate of return, such as being equal to the current U.S. Treasury Bill return + 8% or so.
So how much is $10 a year from now, worth to you today, if you seek a 10% rate of return on your money? The answer is $9.09. If you had $9.09 right now, and you could invest that money at an annual rate of 10%, then you could turn that $9.09 into $10 in one year, since $9.09 multiplied by 1.1 equals $10. So $10 one year from now is only worth $9.09 to you today. In this scenario, $10 in a year, or $9.09 today, are equivalent.
It was calculated via this equation:
DPV = FV / (1 + r)
here DPV means “discounted present value”, and FV means “future value”, and r is your discount rate (which in this case is 10% or 0.1). The $10 is future value, and you want to know the discounted present value of that ten dollars, so you divide the FV by (1 + 0.1) to get the DPV of that money.
If you wanted to know what $10 that you’ll get in two years is worth today, you make a minor adjustment to that equation, and use DPV = FV / (1 + r)^2, since the discount rate must be applied for two years. The answer is that receiving $10 two years from now is worth $8.26 to you today, since you can take $8.26 and multiply it by 1.1, and then multiply it by 1.1 again, to get $10. In this scenario, $10 in two years, or $8.26 today, are equivalent.
So we see that DPV = FV / (1 + r)^n, for a given future value, where n is years. If we have a series of future cash flows each year, then the equation is this:
DPV = (FV1)/(1+r) + (FV2)/(1+r)^2 + … + (FVn)/(1+r)^n
If you find this part complicated, don’t worry, the Dividend Toolkit includes excel spreadsheets doing the calculations for you. You simply have to plugin the numbers.
Different Stock, Different Discount Rate
As previously mentioned, I customize the discount rate in my calculation according to the company I analyze. I think it makes more sense that way as I would expect a higher rate of return from a company showing more risk and vice-versa. This is at the foundation of any stock valuation process as every investor wants to be rewarded for the risk taken.
The discount rates I use vary between 9% and 12%. A company with stellar numbers that will stabilize my portfolio such as 3M Co (MMM) will be discounted at 9% while a company evolving in a highly volatile environment such as Helmerich & Payne (a drilling company in the oil industry) will require a higher return on my investment and will be discounted at 12%.
The use of a low discount rate (9-10%) obviously leads to more undervalued stocks according to your calculation. This is why it is important to be very cautious about the reasons you discount with such low rate. I’ve read other bloggers going under 9% based on the fact that the current risk-free rate is almost zero and the premium shouldn’t be that high. Unfortunately, while such rationale seems to make sense at first glance, this puts almost all dividend growth stocks in an undervalued position. We all know this isn’t possible.
There are no rules preventing you comparing multiple discount rates for a single stock valuation process. Using different rates will help you assess the direct impact of a 1% change and will expose the right margin of safety. The margin of safety is some kind of buffer between what the stock will really be worth in a year from now and how much you calculated its value at. If you can benefit from a 10-20% margin of safety, you have a very good chance of making a good investment.
Example of Discount Rate Use for Present Value of a Stock
In order to help you understand, I will make a dividend discount model (DDM) calculation example with Johnson & Johnson (JNJ) since everybody knows this company.
Since the company is a well-established dividend aristocrat, I don’t expect JNJ to double its value in the near future. The company is well diversified with a world class brand portfolio and sells in just about every country across the planet. For these reasons, the discount rate used is 9%. I also like to use a double stage DDM to see the impact of a first growth rate for the first 10 years and another for the years after.
I use a DDM with a 7.5% dividend growth rate (matching the past 5 years) for the first 10 years and reduce it to 6% afterwards:
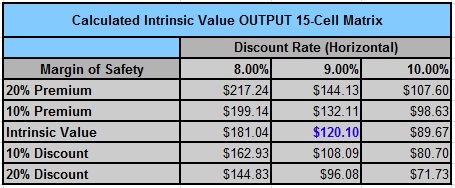 Source: Dividend Toolkit
Source: Dividend Toolkit
The company is currently trading at close to a 20% discount according to my calculation. As you can see, the stock price is completely different if I use a 10% discount rate. In fact, there is a gap of roughly 25% between the fair value with a 9% rate and a 10% rate. A one percent spread makes difference between an undervalued stock by 20% and an overvalued stock by 10%.
This is a good example to show you that the calculation is useful, but can’t be the only reason why you buy or sell a stock. The use of the right discount rate included in a complete stock analysis process will make sense as you will validate your investment thesis with such calculations. This is how you will end-up with a sound investment decision.
Disclaimer: I own shares of JNJ and HP


Hi,
I noticed that for P/E based valuation you have not used time value of money to find PV of estimated stock price at the end of year 10. Please explain.
Hello Rohan,
I’m not sure I understand your question, can you give me more details?
Regards,
Mike.