Discounted Cash Flow Analysis (DCFA) is the bread-and-butter stock valuation method, and is used by world-class value investors like Warren Buffett to determine the fair price to pay for a stock.
In short, the premise of discounted cash flow analysis is that a company is equal to the sum value of all future cash flows, but all of those future cash flows must be translated into their value today, and this translation uses the process of discounting.
An example illustrates the concept concisely:
The Pinball Machine
Suppose you had the business idea to buy a pinball machine and put it in the waiting area of a barber shop, with the permission of the owner. Incidentally, this is what Warren Buffett did as a kid.
The thing is, you have to figure out a fair price to pay for the machine. The estimate will involve two main things: your desired rate of return on your investment, and your estimate for the amount of cash flow that you expect the machine to produce for you. If you pay too much, you’ll get a bad return on your investment, so you need to find a threshold price for which you’ll be willing to buy it.
You estimate that after a year, the pinball machine will produce $1,000 in free cash flows after things like maintenance are considered. You expect that this will stay roughly the same except that it will grow by 3% due to inflation each year. If you expect to leave the machine there indefinitely, how much would you be willing to pay to buy it? Technically if it’s there forever, it’ll produce an infinite amount of money for you, but of course you wouldn’t pay an infinite amount of money for it.
The reason is, money that comes to you next year is worth less to you than the same amount of money right now. Money has a time value. If your target rate of return is 12% per year, and you believe that you could achieve this rate of return with another investment, then $1,000 a year from now is worth only $892.86 to you today, because you could multiply $892.86 by 1.12 to get $1,000 in a year. So the present value to you of $1,000 a year from now is $892.86.
The present value of the $1,030 that you’ll get in two years (the $1,000 that grows by 3% due to inflation for the second year of pinball profits) is even lower. It’s only $821.11, because you could multiply $821.11 by 1.12 and then by 1.12 again, to get $1,030. So $1,030 two years from now is only worth $821.11 to you today.
What we’re doing here is discounting these future values. Each future sum of expected money is discounted by your target rate of return for each year in the future it is, in order to translate it into today’s value to you. This discount rate compensates you for risk and gives you a return on your investment.
The equation that we’re moving towards is that if you buy the machine and put it there forever, and you get to keep all the free cash flows each year, then the machine is currently worth to you a sum equal to all of these future cash flows. But those future cash flows have to be translated into today’s value, because otherwise the sum of future cash flows would be infinite, and because there’s the time value of money. So, the machine’s value is equal to the sum of all future discounted cash flows.
| Year | Cash Flow | Discounted Cash Flow |
|---|---|---|
| 1 | $1,000 | $892.86 |
| 2 | $1,030 | $821.11 |
| 3 | $1060.90 | $755.13 |
| 4 | $1092.73 | $694.45 |
| 5 | $1,125.51 | $638.64 |
…And so on.
It continues infinitely. Here’s a longer version in chart form:
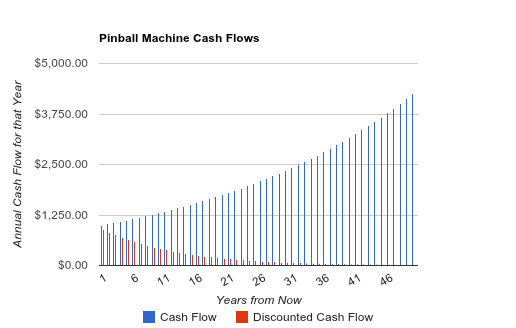
As can be seen, even though the expected cash flow increases each year based on the initial estimate, the discounted value of each cash flow shrinks each year compared to the previous year, because the discount rate of 12% is much larger than the 3% of growth. So even though the machine would technically generate an infinite amount of cash over an infinite amount of time (the sum of all blue lines in the chart, continuing forever), it’s only worth a finite amount of money in today’s value because the sum of discounted future cash flows (the sum of all red lines in the chart, continuing forever) is finite. It’s a calculus limit; only the first few decades matter.
The answer to the original question of how much the pinball machine is worth to you, is approximately $11,111. That’s the sum of all future discounted cash flows, with each year’s cash flow translated into today’s value by discounting it appropriately. If your estimated cash flows are correct, and if that 12% rate of return is your target rate of return for the investment, then that’s how much the machine is worth to you, objectively.
The catch, though, is that you can’t be sure those estimates will be correct. Those estimates aren’t a complete guess, but they’re not guaranteed to be correct either. So discounted cash flow analysis combines art and science. Given correct inputs, it provides objectively correct outputs. But determining reasonable inputs has a bit of an art to it; there’s no objective answer to those from where we stand today.
To balance that out, if you were a pinball investor, you should only buy pinball machines at a discount to the calculated fair buy price, which gives you a margin of safety if your estimates are wrong. (And alternatively, if you’re estimates turn out to be good, then your rate of return will be better than 12%). And you should diversify across numerous pinball machines so that even if one totally breaks, your portfolio of pinball machines is good. The market prices for pinball machines will be all over the place, so you can wait for good deals and pick some up at the right price.
Finding the right stock value before making a purchase
As you can see, using the discounted cash flow analysis is not that easy. The one product I offer on this site is the Dividend Toolkit, which is a comprehensive stock guide that also comes with an easy-to-use valuation spreadsheet to calculate the fair price for dividend stocks. The spreadsheets provide calculation tables to efficiently use both the discounted cash flow analysis and the discounted dividend model. The book along with its spreadsheet will save you time and simply your stock valuation method. You will also find complete information on how to use the calculation table in order to buy stocks at a fair or bargain value.
I know how hard it is to invest when stocks don’t seem to trade at their fair value
Don’t you hate not knowing when to buy or sell stocks? There are too many investing articles contradicting one another. This creates confusion and leaves you with the impression you will not reach financial independence. It doesn’t have to be this way. I’ve built a free recession-proof portfolio workbook which will give you the actionable tools you need to invest with confidence and reach financial freedom.
This workbook is a guide to help you achieve three things:
- Invest with conviction and address directly your buy/sell questions.
- Build and manage your portfolio through difficult times.
- Enjoy your retirement.

